The first law of Complexodynamics

The question that this essay is trying to answer: why does “complexity” or “interestingness” of physical systems seem to increase with time and then hit a maximum and decrease, in contrast to the entropy, which of course increases monotonically? [This was asked in a conference by Sean carroll]

“The interesting middle basically”. To skip to conclusion go to conclusion

The author will draw from Kolmogorov complexity to try and deduce the answer for this.

First of all, What is Kolmogorov complexity? It measures the complexity of any object by the length of the shortest computer program that could describe it. How much simply can you describe the object without loosing information about it.

Why is this more interesting than entropy? While entropy only can capture order, Kolmogorov complexity kinda captures “interestingness” or complexity in a much better way. Perfect order is simple you can capture it easily but complete randomness is also simple(“generate random noise”) but there are more complex things in the middle like say “describe an organism”.

So this is what author wants to do: “

1. Come up with a plausible formal definition of “complexity.”
2. Prove that the “complexity,” so defined, is large at intermediate times in natural model systems, despite being close to zero at the initial time and close to zero at late times.

Not hard to explain why complexity is low in the beginning: Entropy is close to zero. Entropy is sort of an upper bound of complexity really. Not hard to explain the end: We reach a uniform equilibrium. At intermediate though: things are complex because the above constraints don’t hold. So how do we define this large complexity anyway? How high does it get anyway? How to measure it?

The author will use a notion called sophistication from Kolmogorov complexity to define this.

Using Kolmogorov complexity to define entropy Its not obvious as There’s a mismatch in deterministic systems:

• Entropy appears to increase rapidly (linear/polynomial)
• But Kolmogorov complexity only increases logarithmically (log(t))
• This is because you only need: initial state (constant) + time steps (log(t)) Solutions:

1. Use probabilistic systems
2. Use resource bounded Kolmogorov complexity:
   • Add constraints like: time limit, limit of circuit depth, basically resource constraint - severe.
   • Adding this sort of constraint increases the Kolmogorov complexity rapidly in sync with entropy and thus we use it to define it.

How can we define what Sean was calling “complexity”? [from the original quote from now on the author says he will call this “complexotropy”. [Backstory: Kolmogorov observed that what is seemingly complex like a random string is actually also least “complex” or “interesting” . Because you could easily describe it: it’s a random string that’s all it takes to describe it.

But how do we formalise the above intuition.(The sophistication bit actually”)

Given a set S of n-bit stings. K(S) -> number of bits in the shortest program to define this set S Given x an element of S: K(x|S) -> length of shortest program that outputs x given an oracle for testing membership in S. Sophistication of x of Sophistication(x) is the smallest possible value of K(S) over al the sets S such that

1. x ∈ S
2. K(x|S) >= log2(|S|) - c for some contant c.

Basically my understanding is we calculate sophistication by determining a possible K(S) that encompasses x such that the set S is not necessarily describing the randomness of x but still defining the complexity of it.

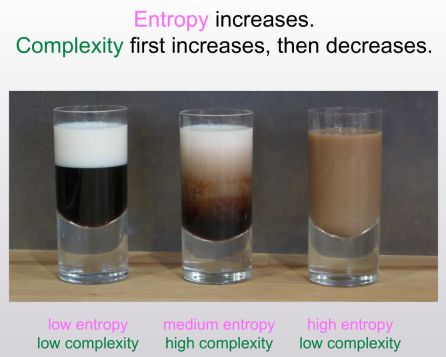
Some example: For the coffee cup above the set can be something like “a mixture of two liquids” it cannot be describing the swirls and the correct patterns in the mixture. So this set determines the sophistication of the x. S shouldn’t be too broad or narrow. Soph(x) is the length of the shortest computer program that defines not necessarily x but S of which x is a random member.

So sophistication seems to capture “complexotropy” well. It defines both simple string and random string to have low sophistication but defines middle to have high complexity Problem: But in deterministic systems

• Same issue as earlier.

• Can describe state at time t using just

  • initial state
  • transition rule
  • time t

  So sophistication is not above log(t) + c This is same for probabilistic state.

So sophistication doesn’t capture the intuition of “complexotropy” as well as intended. It doesn’t grow fast enough. We need to find some other way to measure this.

The fix: Constraint on computational resources. New definition: Any program that runs on n log n time. Then the above problem is solved for. So it’s not easy to just define the program by defining initial step and the time steps. Actually forces us to acknowledge the complexity there. Also this need not be *n log n *. It can be any time bound restriction or anything else.

The motivation is define a “complexotropy” measure that assigns a value close to 0 to the first cup and third cup, but large value to second cup. Thus we consider the length of the shortest computer program that not necessarily defines x but the probability distribution D such that x is no longer compressible in respect to D. (So basically x looks like any other ransom sample from D). Like think of the this as something similar to S but with time constraints. S vs D for my understanding: “D is a sophisticated S” S (Set):

• “All possible states of two mixing liquids”
• Just lists possible states
• No time constraint on generating them

⠀D (Distribution):

• “States you get when you actually mix liquids for t seconds”
• Some patterns more likely than others
• Must be able to generate similar patterns quickly
• Your specific cup should look like typical mixing at time t

The progression of ideas has been:

1. Started with basic Kolmogorov complexity (wasn’t good enough)
2. Moved to sophistication with set S (better, but still didn’t grow fast enough)
3. Finally arrived at complexotropy with distribution D (adds requirements that make it work better)

The constraints should be imposed both at sampling program level. And at reconstruction algorithm level. Sampling algorithm: generate samples for D efficiently. otherwise Could just mention initial state, rules, time t Reconstruction algorithm: given a sample/pattern generate it efficiently. Given unlimited time can find x by finding special properties of x.

Together these two restrictions ensure we are defining “complexotropy” properly.

Notes: First of all it’s all conjecture. But it can be proved in some ways though. Two possible approach: Theoretical proof(author don’t know how). Empirical testing: simulate and use a system to prove it over time. Use approximation. Like gzip file size as proxy for complexity. Similar to using compression for Kolmogorov complexity

Conclusion

1. The Core Question:
   • Why do physical systems follow this pattern:
     • Start simple (low complexity)
     • Become complex (peak complexity)
     • End simple again (low complexity)
2. The Path to Answer:
   • Can’t use entropy (only increases)
   • Try Kolmogorov complexity (program length to generate x)
   • Introduce sophistication (using sets S)
   • Finally arrive at complextropy (using distribution D with constraints)
3. Key Concepts:
   • Sophistication: Measures structure without randomness
   • Complextropy: Sophistication + two efficiency requirements:
     • Must generate samples efficiently
     • Must reconstruct specific state efficiently
4. Important Requirements:
   • Need resource constraints (like time limits)
   • Need bounds on how specific/general our descriptions can be
   • Without these, complexity doesn’t grow enough
5. Practical Testing:
   • Can use simplified models (2D pixel grid)
   • Can use compression (like gzip) as approximation
   • Still an open problem for rigorous mathematical proof
6. Key Insight:
   • Complexity isn’t just about randomness or order
   • Most interesting complexity happens in between
   • Like the middle coffee cup - not ordered, not random, but structured

⠀